El giro de la bóveda celeste

Nuestra Tierra gira. Eso que nos enseñan de pequeños ahora y comprendemos perfectamente fue motivo de grandes discusiones hace varios siglos. Hasta el siglo XVI la teoría aceptada era que La Tierra era el centro del universo y todos los astros giraban a su alrededor. En una noche clara, observamos girar las estrellas y así lo parece. Sin embargo, el giro de la bóveda celeste es provocado por el movimiento de rotación de la Tierra.

Imaginemos que giramos sobre un taburete, todos los objetos que nos rodean parecen girar a nuestro alrededor, cuando, en realidad, somos nosotros los que giramos y no ellos. Si miramos al techo, al punto vertical sobre la cabeza, vemos que dicho punto permanece inmóvil. Eso se explica porque se encuentra en la línea que hace de eje de nuestra rotación.

Esta sencilla explicación sirve para entender el movimiento de la bóveda celeste. Toda ella gira. Las estrellas describen en su movimiento trayectorias que son circunferencias. En el centro de todas esas circunferencias está el polo celeste, que es la línea de nuestro eje de giro.

A veces he escuchado decir que la estrella Polar es la más brillante del cielo. Eso no es cierto. Hay muchas estrellas más brillantes e interesantes en el cielo. Lo que hace especial a la estrella Polar es que, por casualidad, brilla bastante para verla a simple vista y se encuentra muy cerca del polo celeste. No exactamente en el mismo polo, pero lo suficiente como para que la circunferencia que describe en el cielo sea tan pequeña que nos parece inmóvil.

Si dejamos una cámara fotográfica expuesta durante horas apuntando hacia el polo celeste, obtendremos la imagen de los trazos que dejan las estrellas en su movimiento. Los trazos serán más o menos largos según haya durado la exposición. Todos ellos son circulares y concéntricos, siendo su centro el polo celeste. El trazo de la estrella Polar es muy pequeño y está casi en el centro, como puede observarse en la imagen siguiente.

La rotación del cielo se evidencia en esta toma de dos horas.

18-07-1998, Película Fuji 800 ASA desde Casinos (Valencia)

Ya sabemos pues el motivo por el que la estrella Polar es la única estrella que nos parece inmóvil en el cielo. Esto ocurre porque está alineada con el eje de rotación de la Tierra. La estrella Polar nos indica siempre el Norte y todas las estrellas parece que giraran a su alrededor. Esta propiedad ha sido utilizada desde hace miles de años por todas las culturas para ayudarse en la orientación de navegantes y viajeros.

Como podemos considerar que la estrella Polar está inmóvil y todas giran 1 vuelta cada día a su alrededor, podemos llegar a conocer la hora mirando las posiciones de las estrellas.

El reloj estelar

El reloj estelar será una esfera imaginaria cuyo centro, como no, será el polo celeste, que consideraremos por aproximación en la estrella Polar. De allí partirá una línea imaginaria (nuestra manecilla de las horas) que pasará por las dos estrellas exteriores del carro de la Osa Mayor (UMa).

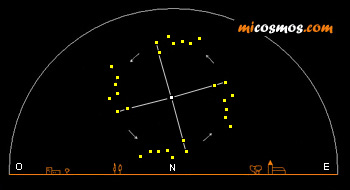
Las dos estrellas del extremo del carro

indican la posición de la estrella polar.

Nuestro reloj se encuentra dividido en 24 partes en lugar de las habituales 12, es decir, que nuestra manecilla emplea 24 horas en completar una vuelta completa y lo hace en el sentido contrario al habitual, por lo que los números están del revés respecto a los que empleamos normalmente.

Reloj estelar

Como la Tierra completa una vuelta cada 23 horas y 56 minutos, el reloj estelar adelanta 4 minutos cada día o, lo que es lo mismo cada 15 días adelanta 1 hora, o cada mes 2 horas.

El 7 de marzo, a las 12 de la noche, nuestro reloj estelar marca las 0 horas, fecha en que coincide. Pero dos semanas después marcará las 0 horas cuando en nuestro reloj de pulsera aún serán las 23 horas.

Ejemplo 1

Imaginemos estamos a 19 de diciembre y que nuestro reloj estelar marca las 20 horas. Con lo explicado anteriormente habrá que efectuar las siguientes correcciones: contaremos el tiempo que ha transcurrido en el calendario desde el 7 de marzo, y restaremos a la hora de nuestro reloj estelar 2 horas por cada mes, 1 hora por cada medio mes y 4 minutos por cada día.

De este modo obtenemos: han transcurrido 9 meses y 12 días, o sea que el desfase es de 9x2=18 horas, y 12x4=48 minutos, que restamos de las 20 horas leídas, resultando que es la 1 de la mañana y 12 minutos, hora solar. En verano le añadimos 2 horas más y en invierno 1 para pasar a hora civil. Como es diciembre, sumamos 1 hora y son las 2 horas y 12 minutos de la mañana.

Ejemplo 2

El 7 de Junio el reloj estelar marca las 2 de la mañana. Como han transcurridos 3 meses desde el 7 de marzo, restamos 3x2=6 horas a la hora leída, por lo que son las 20 horas en horario solar y, por ser horario de verano, sumamos 20+2=22. Luego son las 10 de la noche en nuestro reloj de pulsera.

Con lo visto, concluimos que el reloj estelar nos da una hora aproximada, ya que en los cálculos hemos considerado todos los meses con la misma duración. Para ser exactos deberíamos haber contado los días transcurridos y multiplicar por los 4 minutos diarios de adelanto. 

También influye la posición geográfica del observador respecto del meridiano de Greenwich. Por cada grado de longitud hay que corregir 1 minuto, sumándolo si es al Oeste de Greenwich y restándolo si es al Este.

En cualquier caso, como la hora no puede ser mayor de 24, si el resultado obtenido fuera mayor, se le restará 24.